Finite State Autonoma

What:

A model used to represent and control the execution flow in a system with a finite number of states.

Components:

1. States ($Q$): The finite set of states the automaton (system) can even be in
2. Alphabet ($\Sigma$): The finite set of input symbols
3. Transition Function ($\delta$): A function that defines how the state changes based on inputs it’s gotten.
4. Start State ($q_0$): The initial state the automaton begins.
5. Accept States ($F$): A set of states that determine when an input is accepted.

Example:

Let’s say we want an automaton that accepts the string "ab".

• States: {q₀, q₁, q₂}
• Alphabet: {a, b}
• Transitions:
  • q₀ → a → q₁
  • q₁ → b → q₂
  • q₂ is the accepting state.

If we input "ab", we reach q₂, so it’s accepted. If we input "aa", it gets stuck and is rejected.

It Gets Harder:

1. Deterministic Finite Automaton (DFA):
   • For each state and input symbol, there’s exactly one possible transition.
   • There are no $ϵ$-transitions.
2. Non-Deterministic Finite Automaton (NFA):
   • A state may have multiple transitions for the same input.
   • Some transitions may occur without input ($ϵ$-transitions)
3. Probabilistic Finite Automaton (PFA):
   • Each transition has a probability rather than being deterministic.
4. Pushdown Automaton (PDA):
   • Like an FSA, but using a stack, allowing it to handle more complex languages, e.g. context-free grammars.

Converting from Regular Expressions to DFA:

Overview:

1. Convert from RE to NFA: We do this because RE has implicit non-determinism ($ϵ$-transition).
2. Convert the NFA to DFA: We’ll be left with some left-over states after this.
3. Simplify the DFA: Remove the unnecessary left-over states.

1. Convert RE to NFA

RE	Corresponding NFA
a	Single-state transition: q0 → a → q1
AB (Concatenation)	Connect final state of A to start state of B using an ε-transition.
A|B (Union)	Use ε-transitions to branch into A or B.
A* (Kleene Star)	Create a loop using ε-transitions to allow repetition or skipping A.
A+ (Kleene Plus)	Similar to A*, but requires at least one occurrence of A.
A? (Optional)	Use an ε-transition to optionally skip A.

Example: Convert a* to NFA

For a* (zero or more occurrences of a):

1. Create a new start and accepting state.
2. Add ε-transitions to allow:
   • Skipping "a" (direct ε-transition from start to accept).
   • Repeating "a" by looping back to itself.

NFA Diagram for a*:

(q0) --ε--> (q1) --a--> (q2) --ε--> (q1)
(q1) --ε--> (q3)   (q3 is the final state)

2: Convert NFA → DFA (Subset Construction)

Subset Construction Algorithm

1. Compute ε-closures:
   • The ε-closure of a state is the set of all states reachable via ε-transitions.
2. Define the initial DFA state as the ε-closure of the NFA’s start state.
3. Process each DFA state:
   • Compute transitions for each input symbol.
   • The new state is the ε-closure of the set of NFA states reached.
4. Mark final states:
   • If any state in the DFA contains an accepting NFA state, it becomes an accepting DFA state.
5. Repeat until no new states are generated.

---

Example: Convert NFA (for a*) to DFA

NFA for a* (from Step 1):

(q0) --ε--> (q1) --a--> (q2) --ε--> (q1)
(q1) --ε--> (q3)  (q3 is accepting)

Subset Construction

NFA State Set	Input a	Resulting DFA State
{q0, q1, q3}	a	{q2, q1, q3}
{q2, q1, q3}	a	{q2, q1, q3}

Since {q1, q3} contains the accepting state (q3), the corresponding DFA state is also accepting.

Thus, the DFA for a* is:

(q0) --a--> (q1)
(q1) --a--> (q1) (loops)
(q1 is accepting)

---

Step 3: Minimise the DFA

Once we have the DFA, we can minimise it by:

1. Removing unreachable states.
2. Merging equivalent states (states that behave identically).

Minimisation Algorithm

1. Partition states into two groups:
   • Accepting states.
   • Non-accepting states.
2. Refine partitions:
   • Two states are equivalent if they transition to the same group for all inputs.
   • Merge equivalent states.
3. Construct the minimised DFA.

Example: Minimising a DFA

Consider this DFA:

(q0) --a--> (q1) --a--> (q1)
(q1) --a--> (q1)
(q1 is accepting)

Since q1 is the only useful state, the minimized DFA is simply:

(q0) --a--> (q1)
(q1) --a--> (q1) (loops)

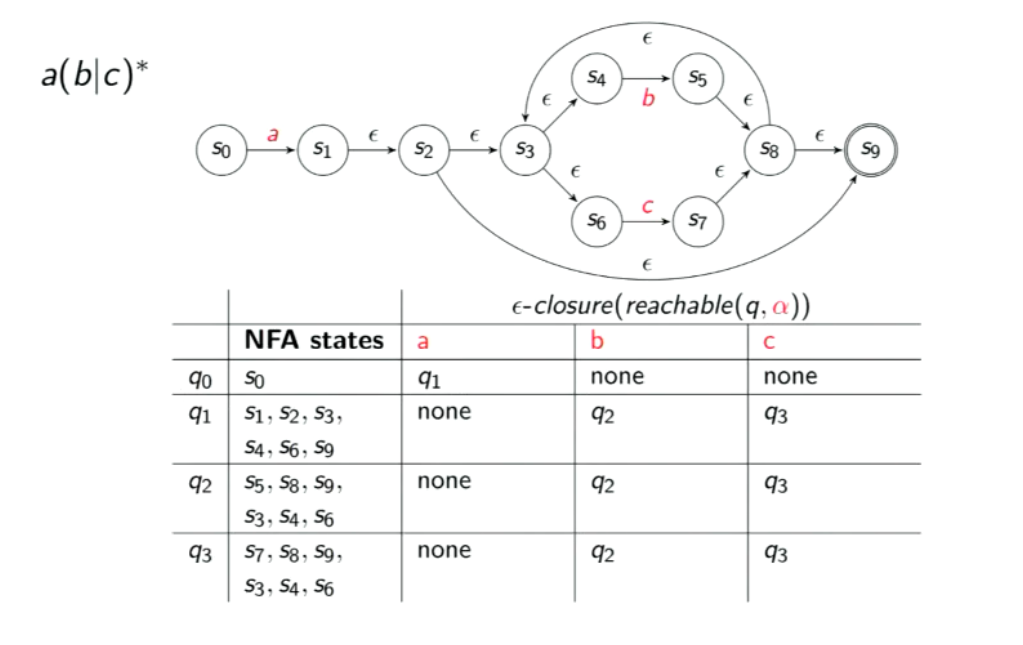
NFA for a(b|c)*:

$q_0$ is the set of all w possible states reachable from $s_0$, given an input $\alpha$.