Premise:
Larger models presented new problems:
- It’s infeasible to train multiple large models to find the best hyperparameters. (i.e. grid search for hyperparameters wouldn’t work).
- If we’ve been given a fixed budget for compute, should we increase the model size or the number of training steps?
- We don’t know when to stop training.
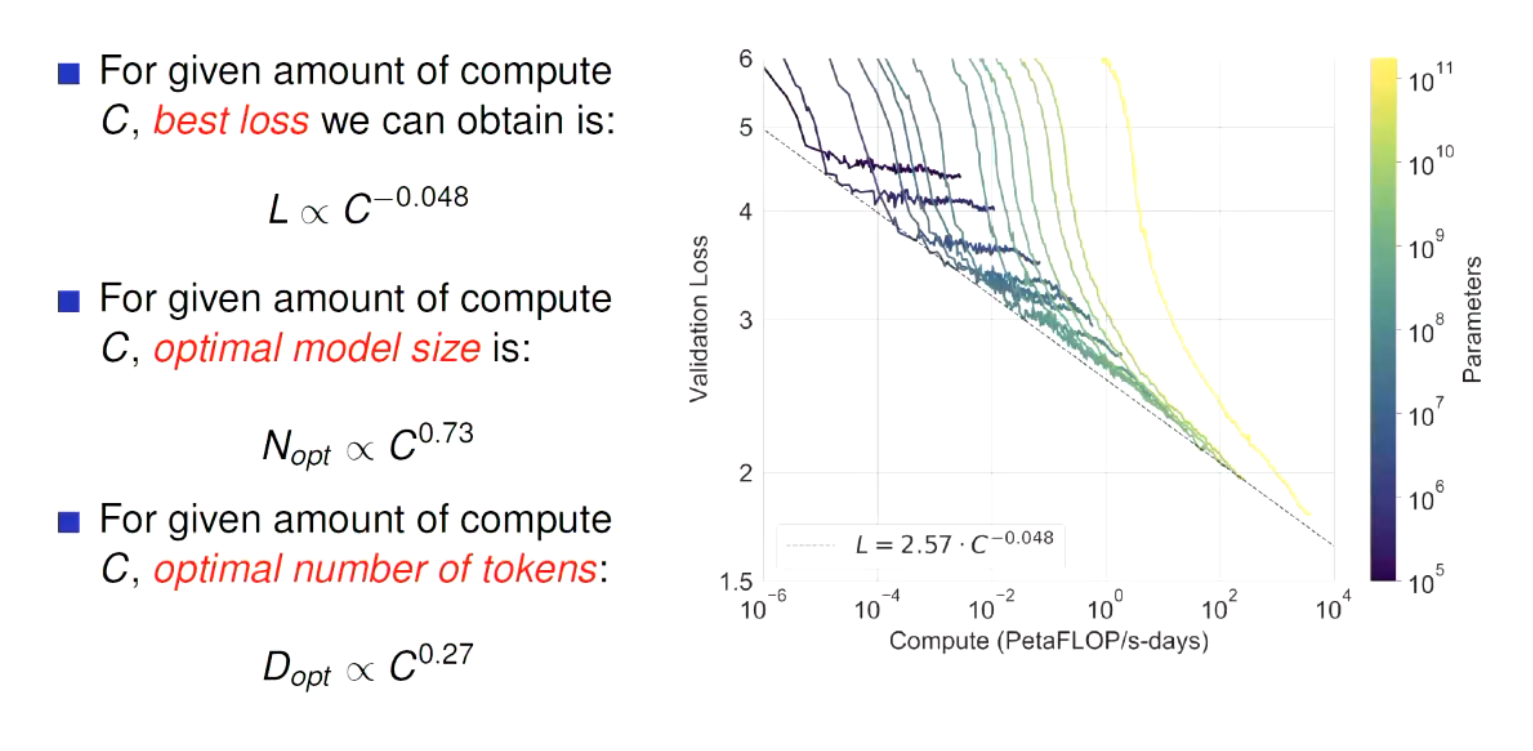
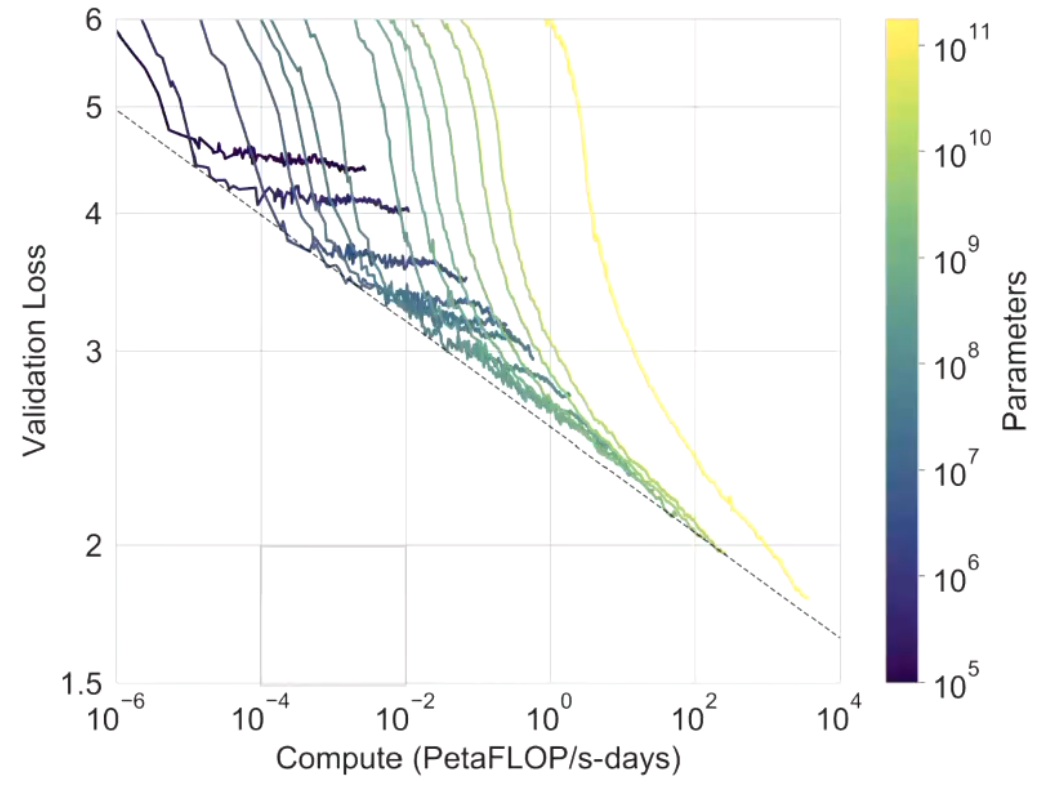
Is there a connection between loss, model size and compute steps?
Background:
Well researchers at OpenAI tried to answer that. They trained differently sized models with different amounts of parameters, for different lengths of time. They found:
- Smaller models don’t have the capacity to take advantage of the extra compute
- Larger models get lower losses, but only after the extra compute.
- There’s a shoulder, at which point these models are not training optimally.
So again, they asked themselves:
Is there a connection between loss, model size and compute steps, specifically for optimality?
Implementing that into real training:
We can’t just train large models willy-nilly. So they claimed:
Test loss is a power law function of model size and compute. Therefore, small models can fit the constants. This can then be extrapolated to larger sizes.
They discovered: